МОСКВА, 5 дек – РИА Новости. Российский математик и его коллега из Израиля доказали многомерную версию "теоремы о дощечках", постулирующей, что шар можно полностью покрыть выпуклыми полосками, совокупная ширина которых будет составлять, как минимум, половину длины его самой большой окружности. Доказательство было опубликовано в журнале Geometric and Functional Analysis.
Эта теорема, как отмечает ученый, является важнейшей частью так называемой дискретной геометрии – особого раздела математики, который изучает, как соотносятся друг с другом геометрические фигуры, их комбинации и наборы. К примеру, она позволяет ответить, какое наибольшее число шаров одинакового размера можно разместить вокруг одного такого же шара. Многие подобные задачи имеют важное практическое значение, так как напрямую связаны с проблемами в IT, физике и химии.
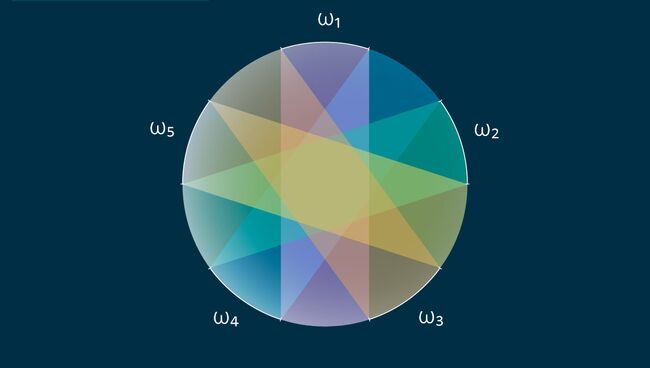
Одна из главных задач, которую изучают представители этой области математики — так называемая "теорема о дощечках", сформулированная еще в начале 20 века. В самом простом виде она гласит, что круг любых размеров невозможно покрыть дощечками, чья общая ширина меньше диаметра самой окружности. Простые варианты этой задачи, как пишут Полянский и его коллега Цзылинь Цзян, более 50 лет назад решили Альфред Тарский и Трегер Банг.
Более сложную версию теоремы выдвинул в 1973 году венгерский математик Ласло Фейеш Тот, который предположил, что сферическую поверхность любых размеров можно покрыть определенным набором трехмерных выпуклых "дощечек", похожих по форме на тонкие полоски кожуры арбуза, чья общая толщина составит как минимум половину длины самой большой окружности.
Авторам статьи, опиравшимся на идеи, которые использовал Трегер Банг для доказательства первой многомерной версии "теоремы о дощечках", удалось не только решить задачу Фейеша Тота, но и показать, что его гипотеза будет работать в многомерном пространстве.
Российский и израильский математики, как и Банг, шли в своем доказательстве от противного: они предположили, что суммарная ширина "дощечек", полностью покрывающих сферу, будет меньше половины длины окружности, и хотели получить противоречие в виде точки, которая лежала бы на сфере, но не была покрыта "дощечками".
Подобные противоречия были найдены, что доказало справедливость идей венгерского математика. Как считают исследователи, их доказательство ускорит развитие дискретной геометрии и позволит сформулировать ряд новых математических и практических задач, связанных с "теоремой о дощечках" и гипотезой Фейеша Тота.