МОСКВА, 24 окт — РИА Новости, Ольга Коленцова. Российские ученые из Нижегородского государственного университета имени Н.И. Лобачевского при поддержке Российского научного фонда усовершенствовали метод глобальной оптимизации, носящий название "диагональный подход". Задачей глобальной оптимизации называют поиск оптимальных решений в различных областях человеческой деятельности. Преимущество диагонального подхода перед иными методами в его быстроте.
При решении многопараметрических прикладных задач существует необходимость расчетов, которые могли бы обеспечить нахождение оптимального решения. Так называется решение, которое даст максимум пользы при минимуме затрат. Поиск математического аппарата для таких расчетов весьма актуален в мире, где мы ограничены во времени, ресурсах и действиях.
Допустим, вы подбираете машину. Она должна быть не слишком дорогой, надежной, иметь автоматическую коробку передач, передний привод, уметь достаточно быстро разгоняться, хорошо управляться и быть симпатичной внешне. Таким образом, имеется набор данных и ограничения, в рамках которых мы выбираем авто. Оптимальное сочетание заданных параметров и является решением задачи глобальной оптимизации, по-другому его можно назвать общим наилучшим результатом расчетов.
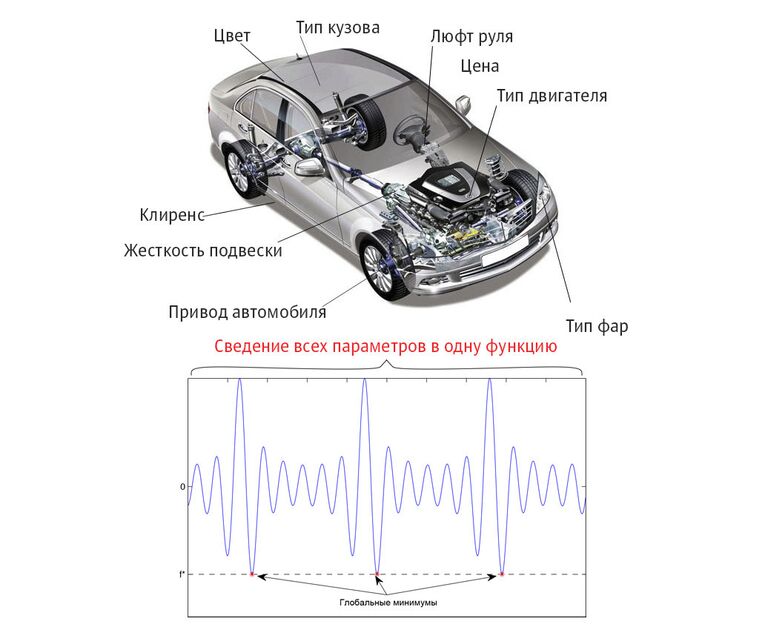
Уровень сложности поставленной задачи оптимизации зависит от числа ограничивающих факторов и рассчитываемых величин. Иногда необходимо учесть только один фактор, а сама структура задачи проста (у нее одно минимальное значение, которое надо найти), с этим легко справляются традиционные математические методы локальной оптимизации.
Возникает необходимость создания новых методов для решения задач глобальной оптимизации, поскольку традиционные алгоритмы с такими задачами не справляются. Компьютеру задается несколько числовых параметров и условия, которые он должен соблюдать при расчете. Системе нужно принять наиболее соответствующее запросу решение, не выходя за рамки поставленных ограничений.
Одним из новых путей решения задачи глобальной оптимизации является диагональный подход. Идею диагональных методов предложил венгерский математик Янош Пинтер в 1996 году, а фундаментальное развитие подхода реализовал российский ученый Ярослав Сергеев, профессор кафедры математического обеспечения и суперкомпьютерных технологий Института информационных технологий, математики и механики Нижегородского государственного университета имени Н. И. Лобачевского. Результаты исследований за последние 20 лет были опубликованы в соавторстве с научным сотрудником того же института Дмитрием Квасовым в монографии "Детерминированная глобальная оптимизация: введение в диагональный подход". Она вышла в издательстве Springer при поддержке Российского научного фонда. За выдающиеся достижения в области математики ученый получил в 2017 году премию имени Хорезми, которую называют "азиатским Нобелем".

Мы разбиваем яблоко на систему меньших гиперкубов, для каждого из них вычисляется числовая характеристика, значение которой определяет его перспективность в продолжении поиска. Далее из всех гиперкубов выбирается гиперкуб с наибольшей характеристикой, который вновь разбивается на множество гиперкубов, и процедура отбора повторяется. Например, если предположить, что все части яблока имеют разный вкус, мы бы отобрали самый сладкий или кислый (в зависимости от того, какой кусочек нам больше нравится).

Принципиальными моментами в этой схеме являются правило вычисления характеристики и способ разбиения наилучшего гиперкуба. В примере с яблоком данное исследование направлено на поиск способов нарезки и выбор самого вкусного фрагмента.
"Наш метод разбиения гиперкубов отличается от традиционных тем, что гиперинтервал разбивается на число подынтервалов, которое можно делить на три (при каждом разбиении возникают три, или девять, или 27 новых подынтервалов). Также диагонали этих гиперкубов вращаются в многомерном пространстве по предложенному нами правилу, в отличие от традиционных методов, где диагонали неподвижны и параллельны друг другу. Это вращение позволяет получить большее количество подынтервалов при уменьшении количества вычислений значений оптимизируемой функции," — поясняет Ярослав Сергеев, разработчик диагонального подхода глобальной оптимизации.

Еще одну особенность разработанного группой Ярослава Сергеева метода (диагонального подхода) можно описать следующим образом — они учитывают качественные особенности в поведении функции, в то время как в традиционном подходе всегда происходит ожидание худшего поведения.
Представьте, что вы гуляете с собакой, которая не прочь подобрать что-нибудь "вкусное" с земли или даже влезть в помойку. Если вы будете постоянно окликать собаку или дергать поводок, то потратите много сил и времени. А если просто внимательно следить за собакой и быть наготове, но при этом не бегать за ней, постоянно заглядывая в пасть, прогулка будет менее затратной по части потери энергии.
Разработанные методы применялись при решении трудоемких реальных задач, например, по оптимизации топологии и обеспечения надежности функционирования коммутируемых сетей, по обработке изображений, оптимальному проектированию систем управления, фильтрации сигналов. Полученные результаты позволили кардинально увеличить эффективность функционирования устройств и систем, реализующих данные процессы.
В настоящее время Ярослав Сергеев с коллегами работает над созданием параллельных вариантов диагонального метода, которые позволят использовать мощные суперкомпьютерные системы для решения задач высокой степени сложности.